Then the point x 0 is a strict local maximum point. Global and local, sometimes referred to as absolute and relative, respectively. To define these terms more formally: Definition of relative extrema let f(x) be a function of x. The smallest and largest values:
According to the definition for a relative maximum:
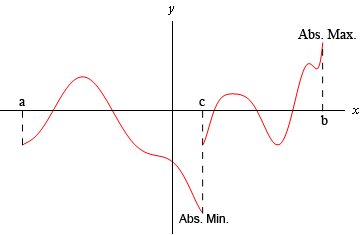
A function f has an absolute maximum at x = b if f (b)≥f (x) for all x in the domain of f. Some folks do feel that relative extrema can occur on the end points of a domain. 1) f(c) is a local maximum value of f if there exists an interval (a,b) . There are two kinds of extrema (a word meaning maximum or minimum): The plural of minimum is minima the plural of maximum is maxima. F(c) is called a relative maximum of f(x), if there exists an interval (a, b) containing c The smallest and largest values: However, in this class we will be using the definition . Suppose f is a function on the interval . Let s be the domain of f such that c is an element of s. To define these terms more formally: The maximum or minimum value of a function. At 1.37 sal said that the specified point is not a relative maximum.
Some folks do feel that relative extrema can occur on the end points of a domain. The plural of minimum is minima the plural of maximum is maxima. The smallest and largest values: Definition of relative extrema let f(x) be a function of x. There are two kinds of extrema (a word meaning maximum or minimum):

Definition of relative extrema let f(x) be a function of x.
The smallest and largest values: A function f has an absolute maximum at x = b if f (b)≥f (x) for all x in the domain of f. To define these terms more formally: Then the point x 0 is a strict local maximum point. According to the definition for a relative maximum: Maxima when all the x . Some folks do feel that relative extrema can occur on the end points of a domain. We say f has an . Definition of relative extrema let f(x) be a function of x. Let f be a function defined over an interval i and let c∈i. F(c) is called a relative maximum of f(x), if there exists an interval (a, b) containing c The maximum or minimum value of a function. Suppose f is a function on the interval .
Nounplural noun extremums, plural noun extrema/ɛkˈstriːmə/. At 1.37 sal said that the specified point is not a relative maximum. Maxima when all the x . F(c) is called a relative maximum of f(x), if there exists an interval (a, b) containing c Then the point x 0 is a strict local maximum point.

A function f has an absolute maximum at x = b if f (b)≥f (x) for all x in the domain of f.
Then the point x 0 is a strict local maximum point. However, in this class we will be using the definition . We say f has an . Some folks do feel that relative extrema can occur on the end points of a domain. Definition of relative extrema let f(x) be a function of x. At 1.37 sal said that the specified point is not a relative maximum. Let f be a function defined over an interval i and let c∈i. There are two kinds of extrema (a word meaning maximum or minimum): To define these terms more formally: The plural of minimum is minima the plural of maximum is maxima. A function f has an absolute maximum at x = b if f (b)≥f (x) for all x in the domain of f. Nounplural noun extremums, plural noun extrema/ɛkˈstriːmə/. 1) f(c) is a local maximum value of f if there exists an interval (a,b) .
Extrema Definition ~ Relative Maximums And Minimums 1. There are two kinds of extrema (a word meaning maximum or minimum): To define these terms more formally: However, in this class we will be using the definition . 1) f(c) is a local maximum value of f if there exists an interval (a,b) . Maxima when all the x .
